Structural Optimisation

Structural optimisation is an integral part of structural design. Every engineer should aim to develop the most cost-effective solution to a given engineering problem. As such computer optimisation techniques have been developed for a long time in an attempt to automate this process. Some authors have attempted to utilise standard optimisation techniques taken from management and industrial optimisation textbooks, whilst others have relied on iterative techniques more similar to how structural solutions are developed in a design practice.

(Christensen PW, 2008) provides a good introduction into the problems of structural optimisations, explaining the main concepts and providing good guidance on the mathematical methods employed in solving basic optimisation problems. It discusses the problems of numerical and shape optimisation, but concentrates mostly on mathematical approaches to numerical optimisation. Simple Structural Optimisation (SO) problems can be represented diagrammatically. Thus where the element functions and limiting criteria can be plotted to indicate the feasible region - it is very easy to visualise how the optimum is found. Whilst not immediately applicable to the application developed it does greatly help in understanding the problem of optimisation:

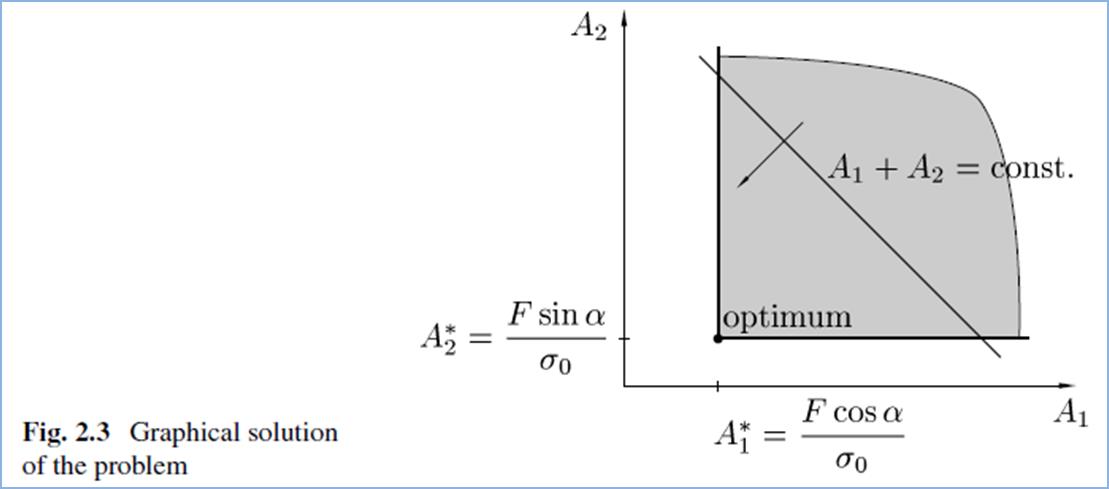
Figure 2‑6 - A graphical representation of a simple two bar optimisation problem showing the limiting conditions reproduced from (Christensen PW, 2008)

Unfortunately, as the structural systems analysed become more complex the optimisation functions get increasingly difficult to plot, and the problems become multi-dimensional. Also it is very difficult to form optimisation functions for arbitrary structures.

An older publication (Haftka & Grandhi, 1986) provides an overview of shape optimisation techniques and a similar publication (Topping, 1983) provides a similar overview for skeletal structures. These divide structural optimisation criteria into size optimisation, topology optimisation and shape optimisation problems. Size optimisation problems seek to minimise section sizes whilst maintaining the fixed geometry (as applicable to this project). Topology optimisation methods generally reduce the number of elements whilst staying within the prescribed optimisation criteria. Finally, shape optimisation algorithms alter the coordinates of nodes. The latter two do not apply to this project.

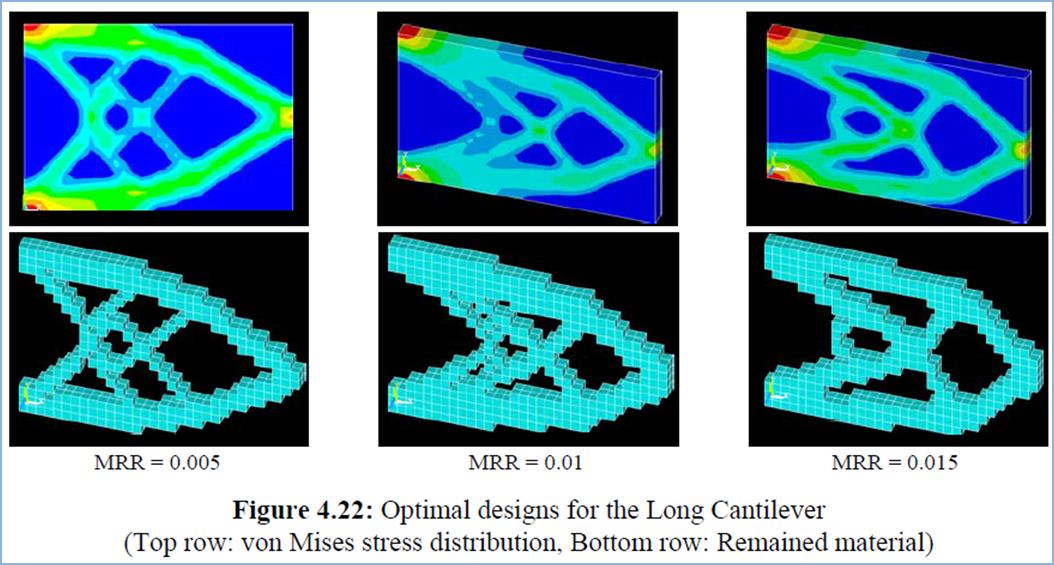
Figure 2‑7 Graphical representation of a typical shape and topology optimisation problem reproduced from (Venetsanos, 2010)

Based on the similar original principles, the structural optimisation methods have been developed since aided by new research as well as the advances in computer technology allowing for more powerful and complicated algorithms to be implemented. The (Venetsanos, 2010) PhD thesis provides a very extensive overview of current research on the topic. The paper acknowledges that the three optimisation methods listed above cannot be easily decoupled and that modern approaches generally adopt a combination of methods with the newer research heavily concentrating on developing shape and topology optimisation procedures.

Another good and recent publication offering extensive information on the topic is (Spillers & MacBain, 2009). It goes into great detail into Sequential Linear Programming and the Incremental Equations of Structures techniques. These are currently most widely used and researched techniques in structural optimisation. Linear programming relies on setting up the problem as a series of linear objective functions subject to linear equality or inequality constraints forming the feasible region - a convex polyhedrona. A suitable linear programming algorithm is then used to find a point a point in the polyhedron where this function has the smallest (or largest) value if such a point exists (Wikipedia, 2013).

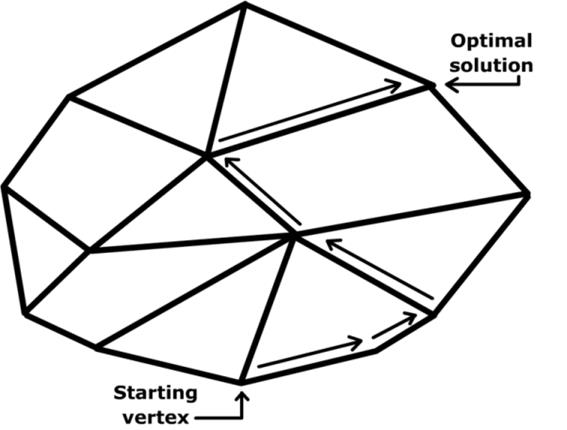
Figure 2‑8 A diagram demonstrating how a Simplex Algorithm is utilised to demonstrate how the optimum solution is found within the polytope

There are numerous mathematical methods developed for optimisation in general. Some are more suitable than others for application than others in the field of structural optimisation. Some of the particular issues include the necessity to utilise the available section sizes, meaning that the potential solution is discretised and not continuous. If using continuous criteria, selecting the closest available selection alters the stiffness matrix from that analysed and can either lead to non-optimal or even non-stable solution. Hence, most structural optimisation techniques rely on iterative approach to a learn7-programming-finite-elements-in-javascript.htm. Also, because there is normally an infinite number of solutions there is a real risk that the optimisation algorithm will reach a local minima, rather than an absolute one. Therefore, the recent advances have relied on introducing the learn7-programming-finite-elements-in-javascript.htm of randomness (similar to mutations in the evolution theory) to ensure that a number of varied solutions are tested in an attempt to truly reach a global optimal solution.

Many of the research papers looking at current developments in Structural Optimisation are printed within the Journal of Structural and Multidisciplinary Optimisation, such as (Mela & Koski, 2012), (Le Riche & Haftka, 2012), and also within other scientific publications (Croce, et al., n.d.) (Talaslioglu, 2009) and many others.

The iterative approach utilised in development of the application is not grossly dissimilar to the approach presented by (Guerlement, et al., 2001). The procedure presented in the paper attempts to find the optimal solution by starting from the heaviest section available and reduces the section to the minimal section that passes ULS and SLS checks. The procedure implemented within the application works in the opposite direction by starting with the smallest available section (for the selected type) and then upgrades the section sizes until all sections meet SLS and ULS criteria. The approach is further detailed below.

Background Information

When sizing each element, a structural engineer normally attempts to select the smallest section that meets the Ultimate Limit State (strength) and the Serviceability Limit State criteria. An iterative technique is often used by engineers to find the optimal solution, whereby an initial section is assumed based on experience and then checked by calculations. If the structural checks fail, the engineer selects a bigger section. On the other hand, if the utilisation of the section is small, the engineer may attempt to justify the use of a smaller section in order to optimise the solution. This is generally a long-winded process and relies on the experience of the engineer to select the initial section and the time constraints required to carry out the necessary iterations.

Outside engineering, optimisation techniques have mostly developed as a part of management studies with the aim of optimising production within a company in order to utilise the company’s resources in the most effective way and maximise profits.  Management optimisation techniques generally attempt to define a problem as a set of mathematical functions, introduce optimisation limits and criteria, and then use mathematical methods to find the optimal solution(s). There are numerous textbooks dealing with this topic as a general problem.

The procedure employed in developing the application uses an approach somewhat similar to the iterative procedure carried out by manual calculations rather than attempting to define the problem mathematically. It relies on the great computational power offered by modern computers.

Optimisation tool in konstrct.com

Whilst it is relatively simple to define an optimisation problem and set up the relevant criteria for specific optimisation problems, it is significantly more difficult to successfully set-up a broad procedure that will work for any (or most) of the assemblies that a user of an application can input.

To illustrate the issue, a simple portal frame problem is presented – an almost infinite number of solutions exist for this problem to include strong column-weak rafter, balanced column-rafter and weak column-strong rafter. Optimising for any route produces local optima, but any of these can be a true global optimal solution. It would not be practical to analyse every possible solution. Finally, changing any of the member properties alters the structure stiffness matrix, and thus the distribution of member forces, and the full analysis must be rerun for every possible case.

As the scope of the project is very broad, a relatively simple iterative technique was adopted. The analysis is initially run with the smallest available section for a chosen section type. Each section is then upgraded to the minimum section that passes ULS checks. The procedure then reruns analysis with the upgraded sections and updated stiffness matrix and reruns all ULS checks and further upgrades sections as necessary. SLS Checks are carried out only if all sections pass ULS checks. This is repeated until all sections pass ULS and SLS checks. The algorithm can optimise each element for minimum weight or minimum section height. A simplified flow diagram of the algorithm is included overleaf to illustrate the procedure.

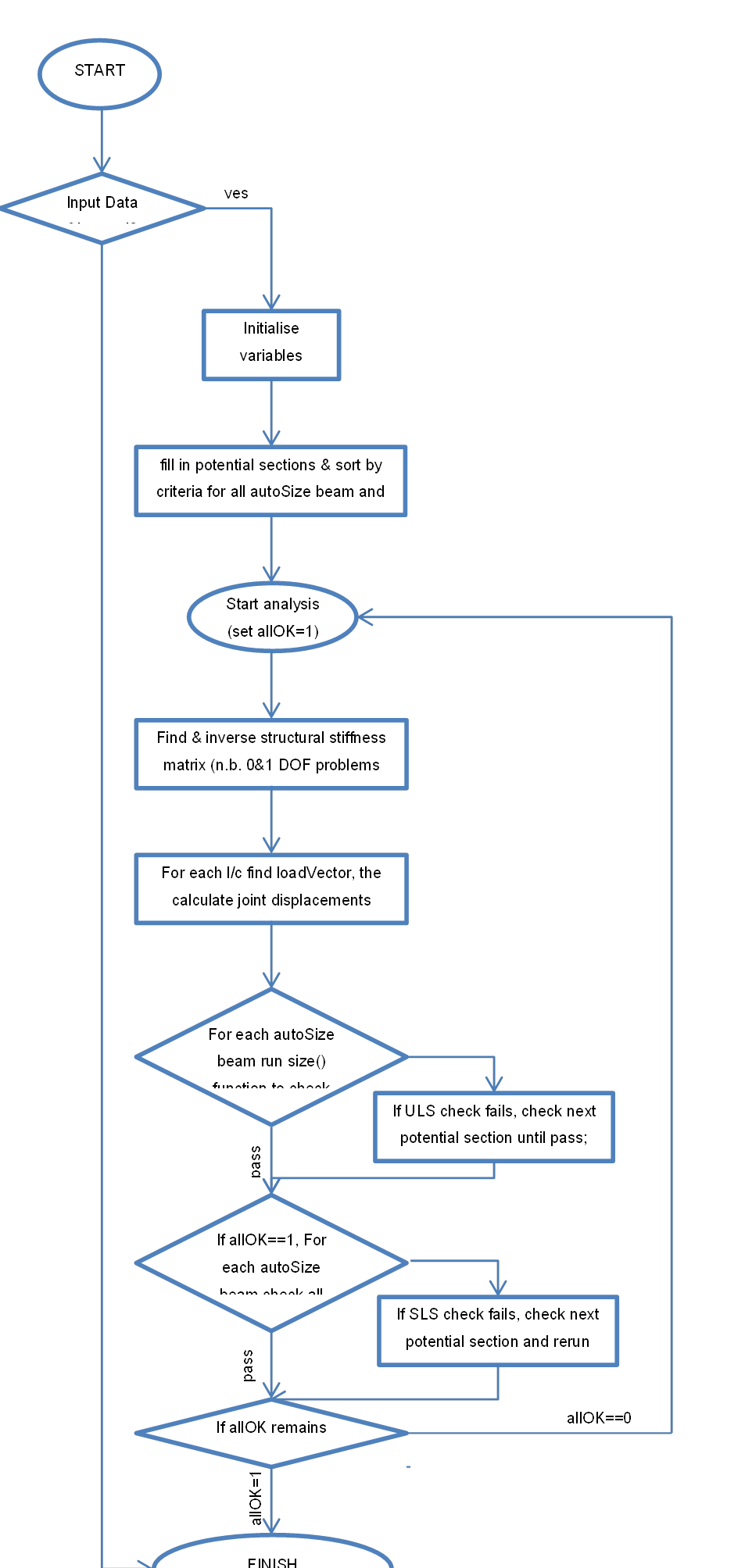
Figure 4‑1 - Outline optimise() function flow diagram

A full EC3 code check is carried out for each ULS check, whereas SLS checks that deflections at any point of the beam do not exceed the prescribed limit. To speed up processing time, simplified capacity checks have been introduced to the ULS sizing algorithm to quickly discard sections that fail simple capacity checks (M/W*py>1.1, N/A*py>1.1, etc), and only perform full checks for sections that are likely to pass.

This approach leads to a fairly balanced result (e.g. in an example of a simple portal frame, leads to similarly sized rafter and column). This returns one of the local minima but for problems with a high learn7-programming-finite-elements-in-javascript.htm of static indeterminacy may not lead to the actual optimal solution. Also the procedure is very resource intensive as it involves carrying out multiple comprehensive EC3 sizing checks which may include Buckling and Lateral Torsional Buckling checks. However, for small assemblies, results are normally presented within a few seconds on a mid-range PC. For structurally determinate systems, and for many indeterminate systems the returned solution is globally optimal.

There is a number of other criteria other than section weight that should be met to truly design the most cost-effective structure. This includes minimising the number of different sections to be used (and thus minimise wastage) or minimising the number of joints (as these are labour intensive and thus expensive). These cannot be simply be implemented within an automated sizing criteria, and a learn7-programming-finite-elements-in-javascript.htm of engineering judgement still remains crucial.

A competent and experienced engineer can and should exercise his engineering judgement to fix the size of certain elements after the initial run to address the criteria above. For example, in order to obtain a truly optimal solution for a portal frame problem presented previously; the engineer can fix an oversized column section and let the algorithm select the matching rafter section. By manually iterating only a few column sections, the engineer should be able to obtain the truly optimal solution for a portal frame. Obviously, extending the structural analysis module to handle non-linear effects would further improve the results!